Introduction

Rotating around a point can be useful in many scenarios in a game, for example we may need to have a planet rotate around its star or an enemy around a player.

In unity the Transform.RotateAround method helps us do that.

But there are situations, where we don’t want the movement to be circular. We may want to move around a certain point and the movement has to be in a diamond shape, or in a hexagon shape.

Instead of having to deal with each of those cases in isolation, let’s see a way that we can make a generic method, that calculates the end point at a certain angle each time. This way we can provide the angle and have the shape we want around a point.

For example, given an angle of 60 degrees, our object will move around the point in the shape of a hexagon, or with an angle of 90 degrees will perform a diamond shape or square movement depending on its starting location compared to the center point.

The first thing we need to do, is to use some basic math, so that we can calculate the rotation given an angle.

Calculating new position given an angle

Here is a basic drawing of what we want to do:

The light blue circle is our object.

The purple circle is the object’s location after we rotate it around the center of our coordinate system (the x and y axis) by angle degrees.

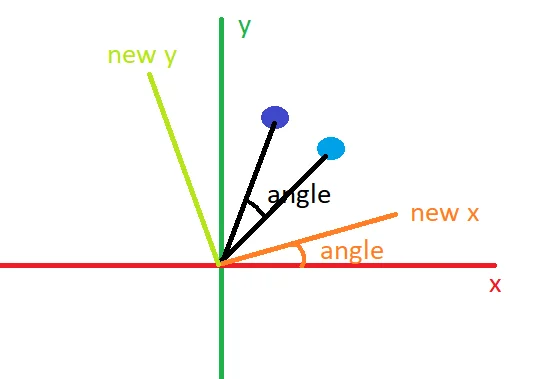
What we actually need to do, is to create a new coordinate system, that is rotated by angle degrees, that is our orange and light green lines (newX and newY)

The angle between the newX axis and the X axis is the same as the angle we need to rotate our object, so the representation of our object in the new coordinate system will also be rotated by angle degrees.

Let’s find first our new X coordinates.

If we represent the newX as our Unit Vector, that is the vector that has a magnitude of 1, then its new coordinates will be (Cos(angle), Sin(angle)) as we can see from the image.

For the Y coordinates, if we accept that our rotation is anti-clockwise we can also find the coordinates: (-Sin(angle),Cos(angle))

So to represent a point in our new system all we have to do is to multiply each coordinate with the new system’s coordinates. If our object has the coordinates of (x,y) its representation in our new coordinate system will be:

newX = X * (Cos(angle), Sin(angle))

and

newY = Y * (-Sin(angle),Cos(angle))

Now the object that we want to rotate around doesn’t have to be in the center of our coordinate system. We just have to move our coordinate system so that its center is the object we want before any calculations by subtracting its coordinates and after any calculations we do the reverse, so that our new system has its center where our old coordinates system had.

Let’s see how we can implement this in Unity:

Implementation in Unity

We need three values:

• A Vector2 with the coordinates of our object.
• A Vector2 with the coordinates of the point we want to move around
• The angle that we want our object to rotate

We can get object’s coordinates with transform.position so our method will have this signature:

Vector2 CalculatePosition(Transform target, float angle, bool clockWise = false)

target is the object which we want to move around, angle is our angle, and the boolean clockWise is the direction we want the rotation to have.

Let’s see the code that will implement the above rotation:

var targetPos = (Vector2)target.position;
var position = (Vector2)transform.position;

var angleInRadians = clockWise ? -angle * Mathf.Deg2Rad : angle * Mathf.Deg2Rad;

we cache the positions in local variables and then depending on the direction of the rotation we need, we calculate the angle in radians.

Then we calculate and cache the Cos and Sin values and we use them to define our new coordinate system.

var cosOfAngle = Mathf.Cos(angleInRadians);
var sinOfAngle = Mathf.Sin(angleInRadians);

var initialVector = new Vector2(cosOfAngle, sinOfAngle);
var perpendicularVectorToInitial = new Vector2(-sinOfAngle, cosOfAngle);

the initialVector is on our new unit Vector along the new X axis and the perpendicularVectorToInitial is our new unit Vector on the new Y axis.

Now we have to subtract the targetPos coordinates from our object’s coordinates, perform the calculations so that we can find its coordinates in our new coordinate system and then add them back:

var newPositionX = (position.x - targetPos.x) * initialVector;
var newPositionY = (position.y - targetPos.y) * perpendicularVectorToInitial;
var finalPosition = newPositionX + newPositionY + targetPos;

The finalPosition here, is the coordinates of our object rotated by angle degrees.

Uses

What we are actually doing is that we find a point where we want our object to move.The way we choose to move to that point is up to us.

For example we may want to move in a straight line and constant speed to that point, or use an easing function. We may even stop at that point perform some action and then calculate the next point.

Here is the full method for easy reference:

Vector2 CalculatePosition(Transform target, float angle, bool clockWise = false)
{
    var targetPos = (Vector2)target.position;
    var position = (Vector2)transform.position;
    var angleInRadians = clockWise ? -angle * Mathf.Deg2Rad : angle * Mathf.Deg2Rad;

    var cosOfAngle = Mathf.Cos(angleInRadians);
    var sinOfAngle = Mathf.Sin(angleInRadians);

    var initialVector = new Vector2(cosOfAngle, sinOfAngle);
    var perpendicularVectorToInitial = new Vector2(-sinOfAngle, cosOfAngle);

    var newPositionX = (position.x - targetPos.x) * initialVector;
    var newPositionY = (position.y - targetPos.y) * perpendicularVectorToInitial;
    var finalPosition = newPositionX + newPositionY + targetPos;

    return finalPosition;
}

Conclusion

A simple project where this method of rotation is used, can be found in this repository

In this project you can see an example of performing actions after arriving to each point, following / getting away from the player and then starting the rotation and of course everything about the rotation can be changed at run-time.

Thank you for reading and as always if you have any questions or comments you can use the comments section or contact me directly via the contact form or by email, also if you don’t want to miss any of the new blog posts, you can always subscribe to my newsletter or the RSS feed.